Widespread
Problem
January 12, 2016
Subject How to measure the distribution of an attribute among the
nodes of a network?
From LEVALLOIS Clément
Sender Social Networks Discussion Forum
To SOCNET@LISTS.UFL.EDU
Date Tue 11:36
----------------------------------------------
Dear List members,
I need to have a measure of how widespread is the distribution of a node
attribute in a network. Let me explain:
My nodes have a textual attribute, let’s say “preferred flavor for ice cream”
I would like to know to what extent the flavor “raspberry” is a value which
is evenly distributed in the network, or to the contrary, just found in one
community. A low value would mean that only nodes from a subregion of the
network have this taste, a higher value would show an even distribution of
the value across the whole network. I imagine that a difficulty is to account
for the frequency of the attribute: if many nodes of the network have
“raspberry” for the value of the attribute, it will tend to make this value
distributed more widely.
Any help or pointer on this would be very much appreciated!
Thank you, Clement Levallois
A possible measure could be the following:
let V be the set of nodes and U the set of nodes with given
attribute value. Then we define the widespread of attribute as
W = | U union N(U) | / | V |
where N(U) is the set of nodes neighboring some node of U .
| | denotes the cardinality (number of elements) of the set.
Some variations on the proposed widespread measure
W = |U union N(U)| / |V|
1. option - consider also the size of set U
W1 = (|U union N(U)| . |U|) / | V |**2
attains its maximum value 1 iff U = V.
2. option - dominating set (https://en.wikipedia.org/wiki/Dominating_set)
W2 = (|U union N(U)| . |V setminus U|) / (|V|.(|V|-1))
attains its maximum value 1 iff U is the center of a star (a single node
linked to all other nodes).
> Indeed my formulation was not clear. Refining my statement, I think a > possible solution can appear: > > - Being evenly distributed in the network would mean that the distance > (shortest paths) between the nodes bearing this attribute value is > comparably close to the distance between the same number of nodes > randomly picked from the entire set of nodes of the network. > > Does it make sense? 2 things: > - it does not depend on a notion of communities > - I might be wrong but the formulation above seems quite > computationally intensive > > Clement If U is a small community then usually N(U) will have large intersection with U and N(U) setminus U will be relatively small - the value of W will be small. We get large values of W when U is large or U contains hubs - nodes with very large degree. It is very fast. The time complexity is linear in number of links.
Widespread index
Let us show how the proposed widespread indices can be computed in Pajek.
Let S be a selected subset of set of nodes V in a simple (no parallel links) network N = (V,L). With N(S) we denote the set of neighbors of the set S:
N(S) = { u ∈ V : ∃ v ∈ S : (v,u) ∈ L }
and with N+(S) = S ∪ N(S). With n = |V| we denote the number of nodes.
A simple widespread index is
W1(S) = |N+(S)| / n .
We have:
- 0 ≤ W1(S) ≤ 1.
- W1(S) = 1 iff S is a dominating set (Wikipedia). D is a dominating set of a network N = (V,L) iff N+(D) = V.
- if S1 ⊂ S2 then N+(S1) ⊆ N+(S2)
- |N+(S1)| ≤ |N+(S2)| iff W1(S1) ≤ W1(S2).
Related to dominating sets is a domination number γ(N)
γ(N) = min{ |D| : D is a dominating set of N }
for which it holds n ≥ γ(N) ≥ ⌈n/(1+Δ)⌉ ≥ 1, where Δ is the largest (out)degree in N. Even better lower bound is γ(N) ≥ k, where k is the smallest number such that
∑ki=1 (1 + di) ≥ n
where ( di )i is a sequence of outdegrees ordered in decreasing order.
The problem with the definition of W1(S) is that it doesn't consider the size of the set S. Let D* be a minimal dominating set. Then an alternative definition of index could be
W*(S) = |N(S) ∖ S| / |V ∖ D*| = |N(S) ∖ S| / (n - γ) .
It is easy to see that
- 0 ≤ W*(S) ≤ 1 .
- in a weakly connected network: W*(S) = 1 iff S is a minimal dominating set.
- if |N+(S1)| = |N+(S2)| and |S1| < |S2| then W*(S1) > W*(S2).
Unfortunately the problem of determining the domination number γ(N) is NP-complete - there is no efficient algorithm to compute W*. To get an efficiently computable index we could replace γ with 1 (it always holds γ ≥ 1); or, even better, with k:
W2(S) = |N(S) ∖ S| / (n - k) = |N(S) ∖ S| / (n - k) .
It holds:
- W*(S) ≥ W2(S)
- 0 ≤ W2(S) ≤ 1.
- W2(S) = 1 iff S is a minimal dominant and independent (Wikipedia) set with k nodes.
- W*(S1) > W*(S2) iff W2(S1) > W2(S2)
- if |N+(S1)| = |N+(S2)| and |S1| < |S2| then W2(S1) > W2(S2).
Note: In network with non-empty set of arcs the nodes with zero indegree are all in any dominant set. Let D0 be the set of all such nodes. Then we get a better lower bound for γ - it is |D0| + k', where k' is the smallest number such that
∑k'i=1 (1 + di) ≥ n - |N+(D0)| .
Since V ∖ D0 can have zero degree nodes again we iterate the process. The final dis are computed in the final V ∖ D0.
Pajek macro for computing both widespread indices
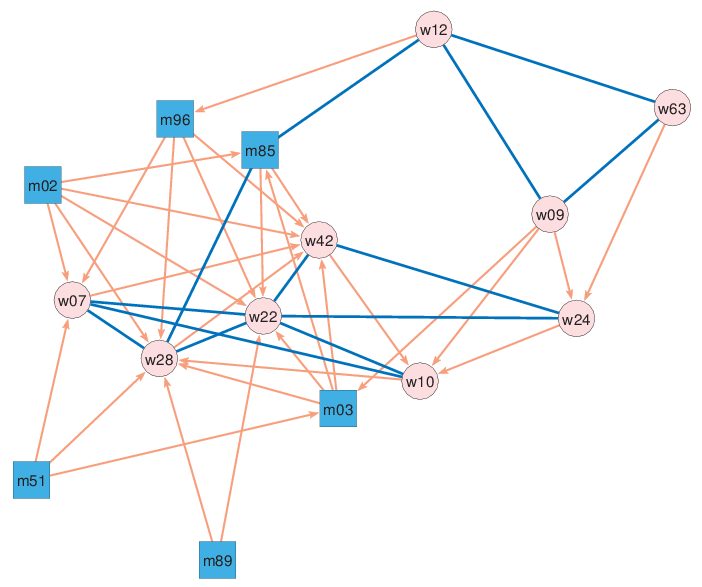
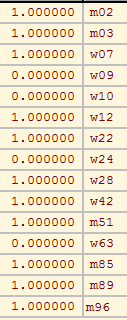
We will illustrate the computation on the case of the subset of boys in the class network.
In Pajek we first read the network and partition the node set to boys and girls according to the node shape (square - boy; circle - girl).
File/Network/Read [class.net]
First, let us determine the lower bound k :
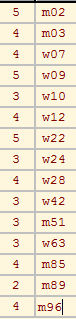
Vector/Create Constant Vector [OK] % e = [1 1 1 ... 1] Vector/Create Scalar/Number % n Select scalar n as Second vector Vectors/Divide (First/Second) % 1 Network/Create Vector/Centrality/Degree/Output % od Select vector e as Second Vectors/Add (First+Second) % od+1 Vector/Make Permutation % sort vector Permutation/Mirror Permutation % in Operations/Vector+Permutation/Reorder Vector % decreasing order Vector/Transform/Cumulatives Vector/Make Partition/by Intervals/Selected Thresholds [15] % enter n Partition/Binarize Partition [1] Partition/Copy to Vector Vector/Create Scalar/Sum % k-1 Select scalar 1 as Second vector Vectors/Add (First+Second) % k File/Vector/Change Label [k]
We get k = 3. It is easy to see that γ = 5.
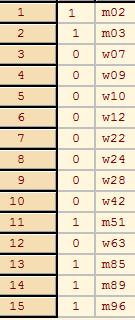
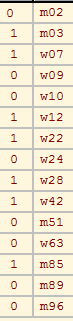
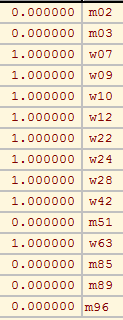
Network/Create Partition/Vertex Shapes Partition/Binarize Partition [1] % 1=boy, 2=girl -> 0=girl, 1=boy
Clicking on the Info button for partition we learn that the group 1 contains 6 boys, and the group 2 contains 9 girls.
Let V = {v1, v2, v3, …, vn}. We assign to its subset S ⊆ V the corresponding characteristic vector χ(S) = [h1, h2, h3, …, hn] where hi = 1 if vi ∈ S, and hi = 0 otherwise.
Partition/Copy to Vector % s = χ(S) Network/Create New Network/Transform/Transpose 1-Mode [yes] % T = transpose N Operations/Network + Vector/Network*Vector [1,OK] % q = T*s File/Network/Dispose % dispose T Vector/Make Partition/by Intervals/Selected Tresholds [0.5] % p1: 1=(q=0), 2=(q>0) Vector/Create Scalar/Number % n Partition/Binarize Partition [2] % p2: 0=(q=0), 1=(q>0) Partition/Copy to Vector % r = χ(N(S)) select vector s as Second vector % Vectors/Max(First,Second) % u = χ(S∪N(S)) Vector/Create Scalar/Sum % np select scalar n as Second vector % Vectors/Divide (First/Second) % W1 = np/n File/Vector/Change Label [W1] % Vector/Create Constant Vector [OK] % e select vector s as Second vector % Vectors/Subtract (First-Second) % C(s) select vector r as Second vector % Vectors/Min (First,Second) % N(S)\S = N(S) ∩ C(S) Vector/Create Scalar/Sum % s' = |N(S)\S| select scalar n as First vector % select scalar k as Second vector % Vectors/Subtract(First-Second) % nd = n - k select scalar s' as First vector % select scalar nd as Second vector % Vectors/Divide (First/Second) % W2 = s'/nd File/Vector/Change Label [W2] %
This sequence of commands is saved as the macro widespread. It expects as “inputs” a network and a subset S
given as a binary partition (characteristic vector). It returns both indices W1 and W2.
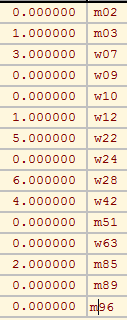
For boys we get: n=15, np=11, s'=5, W1=0.7333, W2=0.4167, W* = 0.5000.
For girls we get: n=15, np=12, s'=3, W1=0.8000, W2=0.2500, W* = 0.3000.
Test files: class.net, wide.mcr (macro without disposes), widespread.mcr ZIP.