Pajek format

Pajek format

A network N = (V,L,P,W) is determined with four sets:

the set of nodes V,
the set of links L,
the set of node properties P, and
the set of link properties (weights) W .

The set of nodes and the set of links describe its structure and form a graph G = (V,L).

A = ∅ - undirected graph
E = ∅ - directed graph

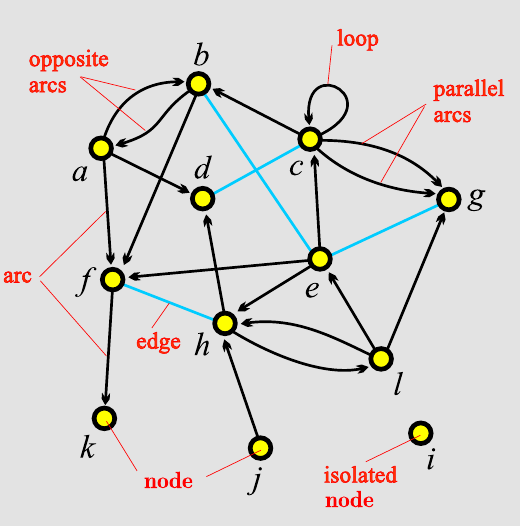
V = { a, b, c, d, e, f, g, h, i, j, k, l }
A = { (a,b), (a,d), (a,f), (b,a), (b,f), (c,b), (c,c), (c,g)₁, (c,g)₂, (e,c), (e,f), (e,h), (f,k), (h,d), (h,l), (j,h), (l,e), (l,g), (l,h) }
E = { (b:e), (c:d), (e:g), (f:h) }
G = ( V, (A, E) )
L = A ∪ E

Sets

The nodes are indexed starting with 1. In listing of links (arcs or edges) their end-nodes are replaced by their indices.

A line describing a node (vertex) has the following components: index, label, X, Y, Z. If the label contains a space it should be put in quotes “la bel”. Pajek's internal coordinates X, Y, Z are in the range [0,1]. If your coordinates are out of this range (for example geographical longitude and latitude) you can transform them into the Pajek's range in the drawing window using the option

Options/Transform/Fit Area

You can even skip the list of nodes - specifying only the line *vertex n. In this case the node labels will be created automatically and the coordinates are put on the circle.

A line describing a link has the following components: 1st-node-index, 2nd-node-index, weight. If the weight is omitted the default value 1 is used.

A line starting with % is a comment line.

% Example network
% by Vladimir Batagelj, April 2003
*Vertices  12
  1 "a"     0.1020  0.3226
  2 "b"     0.2860  0.0876
  3 "c"     0.5322  0.2304
  4 "d"     0.3259  0.3917
  5 "e"     0.5543  0.4770
  6 "f"     0.1552  0.6406
  7 "g"     0.8293  0.3249
  8 "h"     0.4479  0.6866
  9 "i"     0.8204  0.8203
 10 "j"     0.4789  0.9055
 11 "k"     0.1175  0.9032
 12 "l"     0.7095  0.6475
*Arcs
  1  2
  2  1
  1  4
  1  6
  2  6
  3  2
  3  3
  3  7
  3  7
  5  3
  5  6
  5  8
  6 11
  8  4
 10  8
 12  5
 12  7
  8 12
 12  8
*Edges
  2  5
  3  4
  5  7
  6  8

GraphSet: PDF / net; TinaSet: PDF / net, PDF picture.

Neighbors

N_A(a) = { b, d, f }
N_A(b) = { a, f }
N_A( c) = { b, c, g, g }
N_A(e) = { c, f, h }
N_A(f) = { k }
N_A(h) = { d, l }
N_A(j) = { h }
N_A(l) = { e, g, h }
N_E(e) = { b, g }
N_E( c) = { d }
N_E(f) = { h }

N(v) = N_A(v) ∪ N_E(v)

The line with node's neighbors description has a form: i₀, i₁, i₁, …, i_k with a meaning: the node i₀ has neighbors i₁, i₁, …, i_k.

*Vertices  12
  1 "a"   0.1020  0.3226
  2 "b"   0.2860  0.0876
  3 "c"   0.5322  0.2304
  4 "d"   0.3259  0.3917
  5 "e"   0.5543  0.4770
  6 "f"   0.1552  0.6406
  7 "g"   0.8293  0.3249
  8 "h"   0.4479  0.6866
  9 "i"   0.8204  0.8203
 10 "j"   0.4789  0.9055
 11 "k"   0.1175  0.9032
 12 "l"   0.7095  0.6475
*Arcslist
  1  2  4  6
  2  1  6
  3  2  3  7  7
  5  3  6  8
  6 11
  8  4 12
 10  8
 12  5  7  8
*Edgeslist
  2  5
  3  4
  5  7
  6  8

GraphList: PDF / net; TinaList: PDF / net.

Matrix

Our network can be also described using a matrix.

    a  b  c  d  e  f  g  h  i  j  k  l 
 a  0  1  0  1  0  1  0  0  0  0  0  0 
 b  1  0  0  0  1  1  0  0  0  0  0  0 
 c  0  1  1  1  0  0  2  0  0  0  0  0 
 d  0  0  1  0  0  0  0  0  0  0  0  0 
 e  0  1  1  0  0  1  1  1  0  0  0  0 
 f  0  0  0  0  0  0  0  1  0  0  1  0 
 g  0  0  0  0  1  0  0  0  0  0  0  0 
 h  0  0  0  1  0  1  0  0  0  0  0  1 
 i  0  0  0  0  0  0  0  0  0  0  0  0 
 j  0  0  0  0  0  0  0  1  0  0  0  0 
 k  0  0  0  0  0  0  0  0  0  0  0  0 
 l  0  0  0  0  1  0  1  1  0  0  0  0

Graph G is simple if in the corresponding matrix all entries are 0 or 1.

In general, a matrix entry can be any real number. Each matrix line should be written in a single line with at least one space between entries as a separator.

*Vertices  12
  1 "a"    0.1020  0.3226
  2 "b"    0.2860  0.0876
  3 "c"    0.5322  0.2304
  4 "d"    0.3259  0.3917
  5 "e"    0.5543  0.4770
  6 "f"    0.1552  0.6406
  7 "g"    0.8293  0.3249
  8 "h"    0.4479  0.6866
  9 "i"    0.8204  0.8203
 10 "j"    0.4789  0.9055
 11 "k"    0.1175  0.9032
 12 "l"    0.7095  0.6475
*Matrix
 0 1 0 1 0 1 0 0 0 0 0 0
 1 0 0 0 1 1 0 0 0 0 0 0
 0 1 1 1 0 0 2 0 0 0 0 0
 0 0 1 0 0 0 0 0 0 0 0 0
 0 1 1 0 0 1 1 1 0 0 0 0
 0 0 0 0 0 0 0 1 0 0 1 0
 0 0 0 0 1 0 0 0 0 0 0 0
 0 0 0 1 0 1 0 0 0 0 0 1
 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 1 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 1 0 1 1 0 0 0 0

GraphMat: PDF / net; TinaMat: PDF / net, paj.

Special types of networks

Two mode networks

In a two-mode network N=((U,V),L,P,W) the set of nodes consists of two disjoint (sub)sets of nodes U and V, and all the links from L have one endnode in U and the other endnode in V. Often also a weight w : L → ℝ ∈ W is given; if not, we assume w(u,v)=1 for all (u,v) ∈ L.

A two-mode network can also be described by a rectangular matrix A = [a_uv]_U☓V.

Examples:
((persons, societies), years of membership),
((buyers/consumers, goods), quantity),
((parlamentarians, problems), positive vote),
((persons, journals), reading).

A two-mode network is announced by
*vertices n n_U

Authors and works.
The southern women event participation data (Davis) page.

Multirelational networks

A multi-relational network is denoted by N =(V, (L₁,L₂,…,L_k),P,W) and contains different relations L_i (sets of links) over the same set of nodes. Also the weights from W are defined on different relations or their union.

Examples of such networks are: Transportation system in a city (stations, lines); WordNet (words, semantic relations: synonymy, antonymy, hyponymy, meronymy,…), KEDS networks (states, relations between states: Visit, Ask information, Warn, Expel person, …), …

The relation can be assigned to a link in two ways:

add to a keyword for description of links (*arcs, *edges, *arcslist, *edgeslist, *matrix) the number of relation followed by its name:
*arcslist :3 “sent a letter to”
All links controlled by this keyword belong to the specified relation (Sampson, SampsonL).
Any link controlled by *arcs or *edges can be assigned to selected relation by starting its description by the number of this relation
3: 47 14 5
Link with endnodes 47 and 14 and weight 5 belongs to relation 3.

Multi-relational temporal network – KEDS/WEIS

% Recoded by WEISmonths, Sun Nov 28 21:57:00 2004
% from http://www.ku.edu/~keds/data.dir/balk.html
*vertices 325
1 "AFG" [1-*]
2 "AFR" [1-*]
3 "ALB" [1-*]
4 "ALBMED" [1-*]
5 "ALG" [1-*]
 ...
318 "YUGGOV" [1-*]
319 "YUGMAC" [1-*]
320 "YUGMED" [1-*]
321 "YUGMTN" [1-*]
322 "YUGSER" [1-*]
323 "ZAI" [1-*]
324 "ZAM" [1-*]
325 "ZIM" [1-*]
*arcs :0 "*** ABANDONED"
*arcs :10 "YIELD"
*arcs :11 "SURRENDER"
*arcs :12 "RETREAT"
 ...
*arcs :223 "MIL ENGAGEMENT"
*arcs :224 "RIOT"
*arcs :225 "ASSASSINATE TORTURE"
*arcs
224: 314 153 1 [4]                890402  YUG     KSV     224  (RIOT)  RIOT-TORN
212: 314 83 1 [4]                 890404  YUG     ETHALB  212  (ARREST PERSON) ALB ETHNIC JAILED IN YUG
224: 3 83 1 [4]                   890407  ALB     ETHALB  224  (RIOT)  RIOTS
123: 83 153 1 [4]                 890408  ETHALB  KSV     123  (INVESTIGATE)   PROBING
 ...
42: 105 63 1 [175]                030731  GER     CYP     042  (ENDORSE)       GAVE SUPPORT
212: 295 35 1 [175]               030731  UNWCT   BOSSER  212  (ARREST PERSON) SENTENCED TO PRISON
43: 306 87 1 [175]                030731  VAT     EUR     043  (RALLY) RALLIED
13: 295 35 1 [175]                030731  UNWCT   BOSSER  013  (RETRACT)       CLEARED
121: 295 22 1 [175]               030731  UNWCT   BAL     121  (CRITICIZE)     CHARGES
122: 246 295 1 [175]              030731  SER     UNWCT   122  (DENIGRATE)     TESTIFIED
121: 35 295 1 [175]               030731  BOSSER  UNWCT   121  (CRITICIZE)     ACCUSED

KEDS - Kansas Event Data System

Temporal networks

A temporal network N_T =(V,L,P,W, T) is obtained if the time T is attached to an ordinary network. T is a set of time points t ∈ T.

In temporal network nodes v ∈ V and links l ∈ L are not necessarily present or active in all time points. If a link l(u,v) is active in time point t then also its endnodes u and v should be active in time t.

We will denote the network consisting of links and nodes active in time t ∈ T by N(t) and call it a time slice in time point t. To get time slices in Pajek use

Network/Temporal Network/Generate in time

Temporal networks - presence

*Vertices 3
1 "a" [5-10,12-14]
2 "b" [1-3,7]
3 "e" [4-*]
*Edges
1 2 1 [7]
1 3 1 [6-8]

Node a is present in time points 5, 6, 7, 8, 9, 10 and 12, 13, 14.

Edge (1:3) is present in time points 6, 7, 8.

* means 'infinity'.

A link is present, if both its endnodes are present.

Time.net; netsJSON

Temporal networks - events

Event	Explanation
`TI` t	initial events – following events happen when
	time point t starts
`TE` t	end events – following events happen when
	time point t is finished
`AV` v n s	add vertex v with label n and properties s
`HV` v	hide node v
`SV` v	show node v
`DV` v	delete node v
`AA` u v s	add arc (u,v) with properties s
`HA` u v	hide arc (u,v)
`SA` u v	show arc (u,v)
`DA` u v	delete arc (u,v)
`AE` u v s	add edge (u:v) with properties s
`HE` u v	hide edge (u:v)
`SE` u v	show edge (u:v)
`DE` u v	delete edge (u:v)
`CV` v s	change property of node v to s
`CA` u v s	change property of arc (u,v) to s
`CE` u v s	change property of edge (u:v) to s
`CT` u v	change (un)directedness of link (u,v)
`CD` u v	change direction of arc (u,v)
`PE` u v s	replace pair of arcs (u,v) and (v,u) by single edge (u:v)
	with properties s
`AP` u v s	add pair of arcs (u,v) and (v,u)
	with properties s
`DP` u v	delete pair of arcs (u,v) and (v,u)
`EP` u v s	replace edge (u:v) by pair of arcs (u,v) and (v,u)
	with properties s

s can be empty.

In case of parallel links :k denotes the k-th link - HE:3 14 37 hides the third edge linking nodes 14 and 37.

*Vertices 3
*Events
TI 1
AV 2 "b"
TE 3
HV 2
TI 4
AV 3 "e"
TI 5
AV 1 "a"
TI 6
AE 1 3 1
TI 7
SV 2
AE 1 2 1
TE 7
DE 1 2
DV 2
TE 8
DE 1 3
TE 10
HV 1
TI 12
SV 1
TE 14
DV 1

Time.tim; Friends.tim.

File/Network/Read Time Events

Pictures in SVG: Terror news - 66 days.

Extended format

See Pajek manual, page 89-95.