Temporal PathFinder

The Pathfinder algorithm was proposed in the eighties \citep{PF88,PF90} for the simplification of weighted networks - it removes from the network all links that do not satisfy the triangle inequality - if for a weighted link there exists a shorter path connecting its endnodes then the link is removed. The basic idea of the Pathfinder algorithm is simple. It produces a network PFnet(W,r,q) = (V,L_PF) determined by the following scheme of procedure

  compute W(q);
  LPF ← ∅;
  for e(u,v) ∈ L:
     if W(q)[u,v] = W[u,v]: LPF ← LPF ⋃ {e}
  endfor

where W is a network dissimilarity matrix and W^(q) = ⊕{i∈1:q : Wⁱ } = (1 ⊕ W)^q is the matrix of the values of all walks of length at most q computed over the Pathfinder semiring (ℝ^*, ⊕, ⊛, ∞, 0) with a ⊛ b = ^r√(a^r+b^r) and a ⊕ b = min(a,b). The value of w_uv(q) in the matrix W^(q) is equal to the value of all walks of length at most q from the node u to the node v.

The scheme of Pathfinder is implemented as the function pathFinder. The temporal version of the statement

   if W(q)[u,v] = W[u,v]: LPF ← LPF ⋃ {e}

is implemented in the function PFcheck using the merging scheme.

The function MatPower(A,k) computes the k-th power of the matrix A.

The time complexity of the Pathfinder algorithm is O(L ∙ n³ ∙ log q) \citep{PFc}.

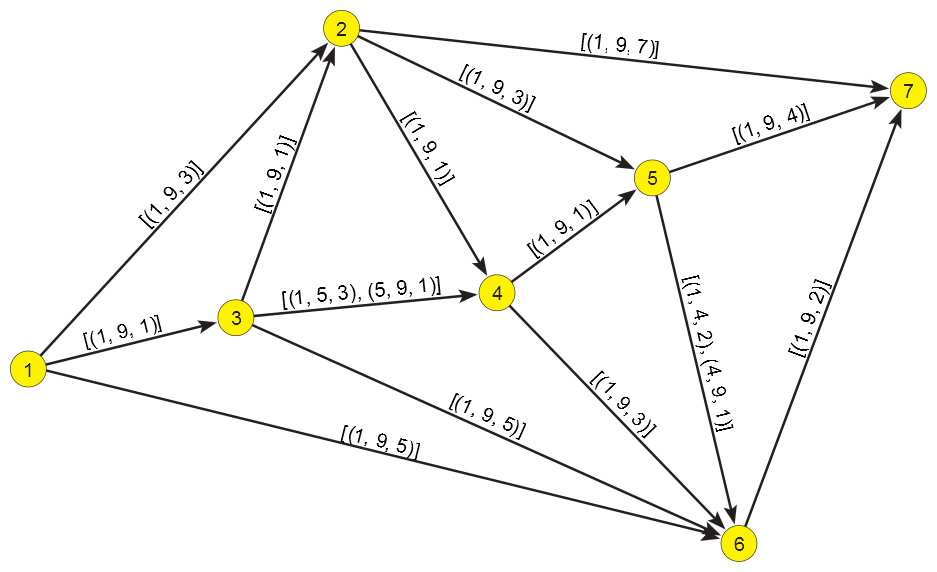
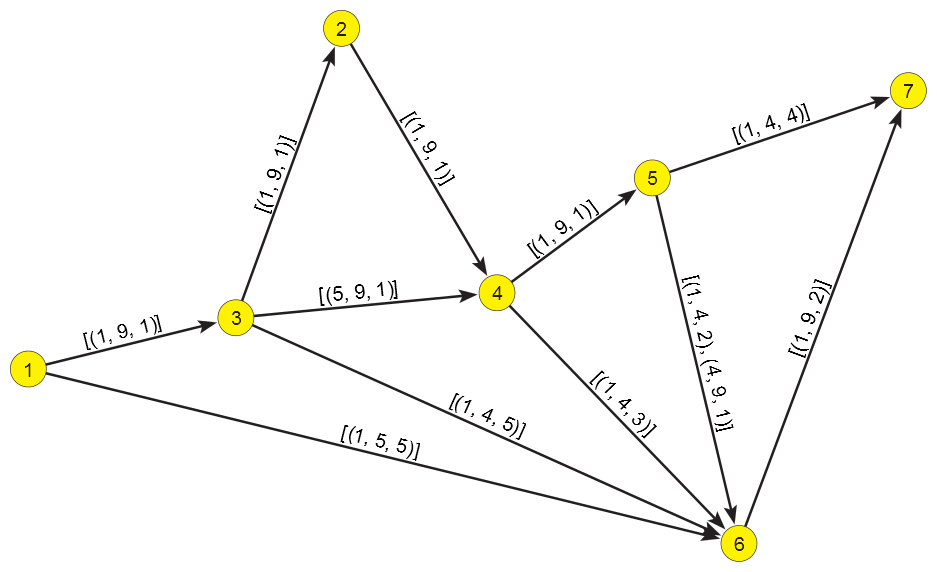
Pathfinder example.

The bottom network in the figure presents the Pathfinder skeleton PFnet(N,1,∞) of a network N presented in the top part of the same figure. Because r=1 a link e is removed if there exists a path, connecting its initial node to its terminal node, with the value (sum of link values) smaller than the value of the link e. The arc (1,2) is removed because 3 = v(1,2) > v(1,3)+v(3,2) = 2. The arc (1,6) is removed in the time interval [5,9) because in this interval 5 = v(1,6) > v(1,3)+v(3,4)+v(4,5) +v(5,6) = 4, etc.