Table of Contents
Derived temporal networks
Networks from bibliographic data
From special bibliographies
(\href{http://www.math.utah.edu/~beebe/}{Bib\TeX})
and bibliographic services
(\href{http://thomsonreuters.com/products_services/science/science_products/a-z/web_of_science/}{Web of Science},
\href{http://www.scopus.com/home.url}{Scopus},
\href{http://sicris.izum.si/default.aspx?lang=eng}{SICRIS},
\href{http://citeseer.ist.psu.edu/}{CiteSeer},
\href{http://www.zentralblatt-math.org/zmath/}{Zentralblatt MATH},
\href{http://scholar.google.com/schhp?hl=en}{Google Scholar},
\href{http://www.informatik.uni-trier.de/~ley/db/}{DBLP Bibliography},
\href{http://www.uspto.gov/}{US patent office},
and others)
we can derive some two-mode networks on selected topics:\\
-- works $\times$ authors ($\mathbf{WA}$),\\
-- works $\times$ keywords ($\mathbf{WK}$);\\ and from some data also the network\\
-- works $\times$ classification ($\mathbf{WC}$), and
the\\-- one-mode citation network works $\times$ works ($\mathbf{Ci}$);\\
where works include papers, reports, books, patents etc.
\medskip
Besides this we get
also at least the partition of works by the journal or publisher and the partition
of works by the publication year.
\medskip
For converting WoS file into networks in \Pajek's format a program
\href{./WoS2Pajek.py}{\WoSPajek} was developed (in Python).
Temporal co-occurrence networks
Let the binary matrix $\mathbf{A}=[a_{ep}]$ describe a two-mode network on the set of
events $E$ and the set of of participants $P$:
\[ a_{ep} = \left\{\begin{array}{ll}
1 & p \mbox{ participated in the event } e \\
0 & \mbox{otherwise}
\end{array}\right. \]
The function $d: E \to \Time$ assigns to each event $e$ the date $d(e)$
when it happened. $\Time = [\func{first}, \func{last}]\subset \NN$. Using these data we can construct two
temporal affiliation matrices:
\begin{itemize}
\item \textbf{instantaneous} $\mathbf{Ai}=[ai_{ep}]$, where
\[ ai_{ep} = \left\{\begin{array}{ll}
[(d(e),d(e)+1,1)] & a_{ep} = 1 \\
\lbrack\ \rbrack & \mbox{otherwise}
\end{array}\right. \]
\item \textbf{cumulative} $\mathbf{Ac}=[ac_{ep}]$, where
\[ ac_{ep} = \left\{\begin{array}{ll}
[(d(e),last+1,1)] & a_{ep} = 1 \\
\lbrack\ \rbrack & \mbox{otherwise}
\end{array}\right. \]
\end{itemize}
Multiplication of co-occurence networks
Instantaneous
Instantaneous $\mathbf{A}$ on $P \times A$ and $\mathbf{B}$ on $P \times B$.
$\mathbf{C} = \mathbf{A}^T . \mathbf{B}$ on $A \times B$.
\[ c_{ij}(t) = \sum_{p \in P} a_{pi}(t)^T \cdot b_{pj}(t) \]
$a_{pi} = [(d_{pi}, d_{pi}+1, v_{pi}) ]$ and $b_{pj} = [(d_{pj}, d_{pj}+1, v_{pj}) ]$
for $t = d$ we get
\[ c_{ij} = [ (d,d+1,\sum_{p\in P: d_{pi}=d_{pj}=d} v_{pi}.v_{pj} )]_{d \in \Time} \]
for $ v_{pi}=v_{pj}=1$ we finally get
\[ v_{ij}(d) = | \{p\in P: d_{pi}=d_{pj}=d \} | \]
For binary temporal two-mode networks $\mathbf{A}$ and $\mathbf{B}$ the value
$v_{ij}(d)$ of the product $\mathbf{A}^T . \mathbf{B}$ is equal to the number
of different members of $P$ with which both $i$ and $j$ have contact in the instant $d$.
Cumulative
Cumulative $\mathbf{A}$ on $P \times A$ and $\mathbf{B}$ on $P \times B$.
$\mathbf{C} = \mathbf{A}^T . \mathbf{B}$ on $A \times B$.
\[ c_{ij}(t) = \sum_{p \in P} a_{pi}(t)^T \cdot b_{pj}(t) \]
$a_{pi} = [(d_{pi}, last+1, v_{pi}) ]$ and $b_{pj} = [(d_{pj}, last+1, v_{pj}) ]$
for $t = d$ we get
\[ c_{ij} = [ (d,d+1,\sum_{p\in P: (d_{pi}\leq d) \land (d_{pj}\leq d)} v_{pi}.v_{pj} )]_{d \in \Time} \]
for $ v_{pi}=v_{pj}=1$ we finally get
\[ v_{ij}(d) = | \{p\in P: (d_{pi}\leq d) \land (d_{pj}\leq d) \} | \]
\end{frame}
Temporal co-authorship networks
Using the multiplication of temporal matrices over the combinatorial semiring we
get the corresponding instantaneous and cumulative co-occurrence matrices
\[ \mathbf{Ci} = \mathbf{Ai}^T \cdot \mathbf{Ai} \qquad \mbox{and}
\qquad \mathbf{Cc} = \mathbf{Ac}^T \cdot \mathbf{Ac} \]
A typical example of such a matrix is the papers authorship matrix $\mathbf{WA}$ where
$E$ is the set of papers $W$, $P$ is the set of authors $A$ and $d$ is the publication
year. \smallskip
The triple $(s,f,v)$ in a temporal quantity $ci_{pq}$ tells that in the time interval
$[s,f)$ there were $v$ events in which both $p$ and $q$ took part. \smallskip
The triple $(s,f,v)$ in a temporal quantity $cc_{pq}$ tells that in the time interval
$[s,f)$ there were in total $v$ accumulated events in which both $p$ and $q$ took part.
\smallskip
The diagonal matrix entries $ci_{pp}$ and $cc_{pp}$ contain the temporal quantities
counting the number of events in the time intervals in which the participant
$p$ took part.
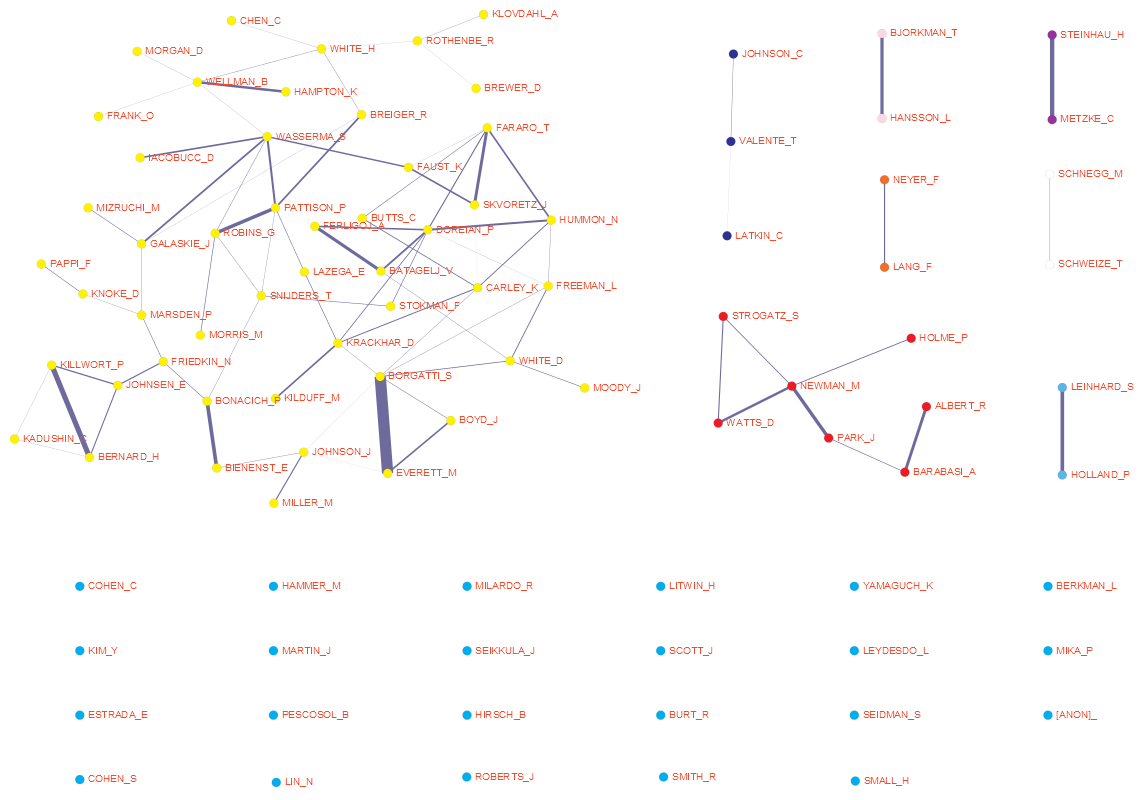
Example: 92 most active socnetters
For an example, from a collection SN5 of network data about
publications on social networks till 2008 we extracted data about 92 the most
active researchers and transformed them to corresponding temporal
networks: CiteInst, CiteCum, WAinst, WAcum, WKinst, WKcum and a partition
W92 with outdegrees of works in the original WA network.
The matrices
\[ \mathbf{Coi} = \mathbf{WAi}^T \cdot \mathbf{WAi} \qquad \mbox{and}
\qquad \mathbf{Coc} = \mathbf{WAc}^T \cdot \mathbf{WAc} \]
describe the instantaneous co-autorship temporal network and the cumulative
co-autorship temporal network.
92 authors
Temporal co-authorship networks
>>> import os, sys, datetime >>> os.chdir("C:/Users/batagelj/work/Python/WoS/SN5/ten") >>> from TQ import * >>> wai = TQ.Ianus2Mat("WAinst.ten") >>> wac = TQ.Ianus2Mat("WAcum.ten") >>> list(wai.keys()) ['dim', 'met', 'typ', 'nam', 'mat', 'til', 'tin', 'tit'] >>> wai['dim'] (1346, 92, 1970, 2008) >>> WAi = wai['mat']; WAc = wac['mat'] >>> AWi = TQ.MatTrans(WAi); AWc = TQ.MatTrans(WAc) >>> Coi = TQ.MatProd(AWi,WAi); Coc = TQ.MatProd(AWc,WAc) >>> auNames = wai['nam'][nr:] >>> ia=dict(zip(auNames,range(92))) >>> Coi[ia['BORGATTI_S']][ia['EVERETT_M']] [(1988, 1989, 1), (1989, 1990, 2), (1990, 1991, 4), (1991, 1992, 1), (1992, 1995, 2), (1996, 1998, 1), (1999, 2000, 3), (2003, 2004, 1), (2005, 2007, 1)] >>> Coc[ia['BORGATTI_S']][ia['EVERETT_M']] [(1988, 1989, 1), (1989, 1990, 3), (1990, 1991, 7), (1991, 1992, 8), (1992, 1993, 10), (1993, 1994, 12), (1994, 1996, 14), (1996, 1997, 15), (1997, 1999, 16), (1999, 2003, 19), (2003, 2005, 20), (2005, 2006, 21), (2006, 2008, 22)]
Authors and keywords
Using the multiplication of temporal matrices over the combinatorial semiring on bibliographic matrices $\mathbf{WA}$ and $\mathbf{WK}$ we get the corresponding instantaneous and cumulative matrices \[ \mathbf{AKi} = \mathbf{WAi}^T \cdot \mathbf{WKi} \qquad \mbox{and}
\qquad \mathbf{AKc} = \mathbf{WAc}^T \cdot \mathbf{WKc} \]
The triple $(s,f,v)$ in a temporal quantity $aki_{ak}$ tells that in the time interval $[s,f)$ the author $a$ used the keyword $k$ $v$ times (in $v$ works). \smallskip
The triple $(s,f,v)$ in a temporal quantity $akc_{ak}$ tells that in an instant $t$ in the time interval $[s,f)$ the author $a$ used cumulatively (till time $t$) the keyword $k$ $v$ times (in $v$ works).
>>> wki = TQ.Ianus2Mat("WKinst.ten") >>> AKi = TQ.MatProd(AWi,wki['mat']) >>> kwNames = wki['nam'][nr:] >>> len(kwNames) 8571 >>> ik=dict(zip(kwNames,range(8571))) >>> Bc = [ AKi[i][ik['centrality']] for i in range(92)] >>> [auNames[i] for i in range(92) if Bc[i]!=[]] ['BORGATTI_S', 'CARLEY_K', 'GALASKIE_J', 'BURT_R', 'FREEMAN_L', 'NEWMAN_M', 'BARABASI_A', 'WELLMAN_B', 'KNOKE_D', 'PAPPI_F', 'HOLME_P', 'WATTS_D', 'JOHNSON_C', 'WHITE_D', 'BREWER_D', 'MARSDEN_P', 'ROTHENBE_R', 'VALENTE_T', 'SNIJDERS_T', 'KRACKHAR_D', 'WHITE_H', 'KILDUFF_M', 'LEYDESDO_L', 'KLOVDAHL_A', 'MOODY_J', 'FRANK_O', 'BONACICH_P', 'BATAGELJ_V', 'JOHNSON_J', 'FAUST_K', 'MIZRUCHI_M', 'YAMAGUCH_K', 'FRIEDKIN_N', 'LAZEGA_E', 'CHEN_C', 'KILLWORT_P', 'ESTRADA_E', 'BUTTS_C', 'EVERETT_M', 'FERLIGOJ_A', 'IACOBUCC_D'] >>> T = [ (i,TQ.total(Bc[i])) for i in range(92) ] >>> I = sorted(T,key=lambda e:e[1],reverse=True) >>> [[auNames[i],v,Bc[i]] for (i,v) in I[:5]] [['BORGATTI_S', 11, [(1991, 1992, 1), (1994, 1995, 1), (1997, 1998, 1), (1999, 2000, 2), (2003, 2004, 1), (2005, 2007, 2), (2007, 2008, 1)]], ['NEWMAN_M', 9, [(2001, 2002, 2), (2002, 2003, 1), (2004, 2005, 2), (2005, 2006, 1), (2006, 2007, 2), (2007, 2008, 1)]], ['BONACICH_P', 7, [(1986, 1988, 1), (1991, 1992, 1), (1998, 1999, 1), (2001, 2002, 1), (2004, 2005, 2)]], ['EVERETT_M', 6, [(1997, 1998, 1), (1999, 2000, 2), (2004, 2007, 1)]], ['CARLEY_K', 5, [(1999, 2000, 1), (2003, 2004, 1), (2006, 2007, 3)]]]
%******************************************************************************
\begin{frame}[fragile]
\frametitle{Temporal citation networks \label{citem}}
\small
A citation matrix $\mathbf{Ci}$ describes the citation relation $p$ cites $q$.
Note that \quad $ p \mbox{ cites } q \Rightarrow d(p) \geq d(q) $.
Then we can construct its instantaneus version $\mathbf{Cii}$:
\[ cii_{pq} = [ (d(p), d(p)+1, 1 ) ] \quad \mbox{iff} \quad ci_{pq} = 1 \]
and its cumulative version $\mathbf{Cic}$:
\[ cic_{pq} = [ (d(p), last+1, 1 ) ] \quad \mbox{iff} \quad ci_{pq} = 1 \]
Temporal versions of:
Bibliographic coupling $\mathbf{biCo} = \mathbf{Ci} \cdot \mathbf{Ci}^T$.
Co-citation $\mathbf{coCi} = \mathbf{Ci}^T \cdot \mathbf{Ci}$.
Citations between authors $\mathbf{Ca} = \mathbf{WA}^T \cdot \mathbf{Ci} \cdot \mathbf{WA}$.
\[ \mathbf{ACA} = \mathbf{WAi}^T \cdot \mathbf{Cii} \cdot \mathbf{WAc} \]
Citations between authors
>>> cite = TQ.Ianus2Mat("CiteInst.ten") >>> Cite = cite['mat']; WAc = wac['mat'] >>> ACA = TQ.MatProd(TQ.MatProd(AWi,Cite),WAc) >>> ACA[ia['WASSERMA_S']][ia['HOLLAND_P']] [(1977, 1978, 1), (1980, 1981, 5), (1981, 1982, 2), (1984, 1985, 2), (1985, 1986, 1), (1987, 1989, 2), (1990, 1991, 1), (1991, 1992, 2), (1992, 1994, 3), (1995, 1996, 2), (1996, 1997, 3), (1999, 2000, 5), (2000, 2001, 1), (2006, 2008, 1)] >>> D = [(i,TQ.total(ACA[ia['DOREIAN_P']][i])) for i in range(92)] >>> J = sorted(D,key=lambda e:e[1],reverse=True) >>> [[auNames[i],v,ACA[ia['DOREIAN_P']][i]] for (i,v) in J[:5]] [['DOREIAN_P', 69, [(1980, 1983, 1), (1984, 1985, 2), (1985, 1986, 1), (1986, 1987, 3), (1987, 1988, 2), (1988, 1989, 7), (1989, 1990, 5), (1990, 1991, 2), (1992, 1993, 6), (1994, 1995, 8), (1995, 1996, 2), (1996, 1997, 4), (2000, 2001, 3), (2001, 2004, 4), (2004, 2005, 6), (2006, 2007, 3)]], ['BREIGER_R', 26, [(1980, 1981, 3), (1984, 1986, 1), (1986, 1987, 2), (1987, 1988, 1), (1988, 1989, 4), (1989, 1990, 1), (1992, 1993, 3), (1994, 1995, 2), (1995, 1996, 1), (1996, 1997, 2), (2000, 2001, 1), (2004, 2005, 2), (2007, 2008, 2)]], ['BURT_R', 20, [(1985, 1986, 3), (1986, 1987, 1), (1987, 1988, 2), (1988, 1989, 5), (1989, 1990, 2), (1992, 1993, 4), (1994, 1995, 1), (2000, 2001, 1), (2004, 2005, 1)]], ['BATAGELJ_V', 17, [(1992, 1993, 2), (1994, 1995, 2), (1996, 1997, 4), (2000, 2001, 4), (2004, 2005, 5)]], ['FARARO_T', 15, [(1984, 1985, 1), (1985, 1986, 2), (1988, 1989, 2), (1989, 1990, 1), (1992, 1993, 1), (1995, 1996, 1), (2001, 2002, 3), (2002, 2003, 2), (2003, 2004, 1), (2006, 2007, 1)]]] >>>
Except where otherwise noted, content on this wiki is licensed under the following license: CC Attribution-Noncommercial-Share Alike 3.0 Unported